Рассмотрим следующую задачу. Пусть при некоторых углах атаки и скольжения, а также заданных параметрах набегающего потока (скорость VҐ, статическое давление PҐ, плотность rҐ и температура TҐ) известно распределение по поверхности обтекаемого тела давления P и касательного напряжения t и требуется определить суммарные значений аэродинамических сил и моментов.
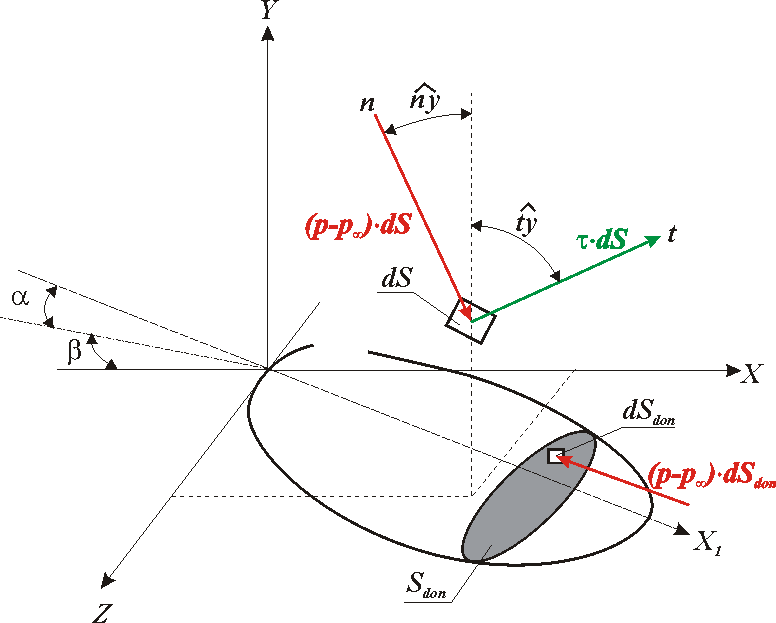
Рис. 1.3.1 Схема действия сил давления и трения на элементарную площадку
На выделенную элементарную площадку dS поверхности тела действуют нормальная сила от избыточного давления (р - pҐ)ЧdS и касательная к площадке сила tЧdS. Сумма проекций этих сил на ось х поточной (скоростной) системы координат равна (рис. 1.3.1)
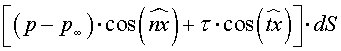(1.3.1)
где n и t - соответственно нормаль и касательная к элементарной площадке.
Две
другие проекций на оси y, z
получаются по аналогичной формуле с
соответствующей заменой косинусов. Чтобы
получить результирующие силы, надо
проинтегрировать выражение (1.3.1) по всей
поверхности S. Введя в полученные
соотношения обозначения для коэффициента
давления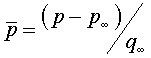 
местного коэффициента трения 
,
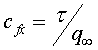где 
-
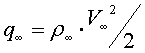скоростной напор, получим следующие
формулы для силы лобового сопротивления,
подъемной и боковой сил:
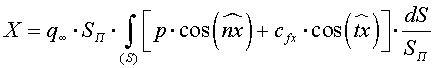(1.3.2)
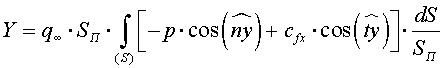(1.3.3)
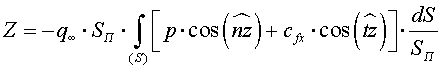(1.3.4)
В этих формулах в качестве характерной площади SП, может быть выбрана произвольная поверхность, например площадь крыла в плане, площадь наибольшего (миделевого) сечения корпуса и др. Интегралы в формулах (1.3.2) - 1.3.4) являются безразмерными величинами, учитывающими влияние на аэродинамические силы характера обтекания тела заданной геометрической формы и обусловленного этим обтеканием распределения безразмерных коэффициентов давления и трения.
В формуле (1.3.2) для силы X безразмерная величина обычно обозначается cx и называется аэродинамическим коэффициентом силы лобового сопротивления. В двух других формулах вводятся соответствующие обозначения величин cy, и cz, первая из которых называется коэффициентом подъемной силы, а вторая - коэффициентом боковой силы. С учетом сказанного
(1.3.5)
Аналогично формулам (1.3.2) - (1.3.4) для сил могут быть получены общие соотношения для моментов. Для примера рассмотрим такое соотношение для момента тангажа Mz. Очевидно, элементарная величина этого момента dMz определяется суммой моментов относительно оси z сил, действующих на площадку dS в плоскости, перпендикулярной оси z. Если координаты площадки dS будут yґx, то элементарная величина момента
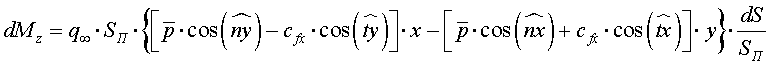
Интегрируя это выражение по поверхности S и вводя безразмерный параметр
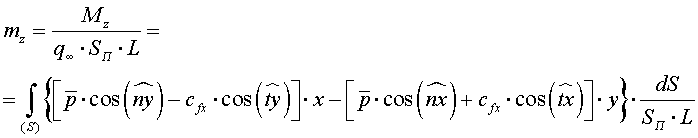(1.3.6)
в котором L - некоторый характерный геометрический размер, получим формулу для момента тангажа:
(1.3.7)
Параметр mz называется аэродинамическим коэффициентом момента тангажа. Аналогично записываются формулы для других составляющих момента:
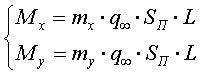(1.3.8)
Безразмерные параметры mx н my называются соответственно коэффициентами моментов крена и рыскания.
Соответствующие аэродинамические коэффициенты сил и моментов могут быть введены и в связанной системе координат. При помощи этих коэффициентов силы и моменты можно представить в следующем виде:
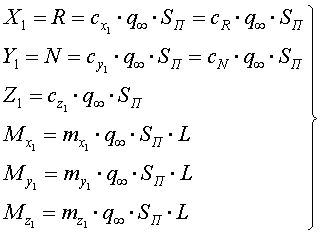(1.3.9)
Величины cx1(cR), cy1(cN), cz1 называются соответственно коэффициентами продольной (осевой), нормальной и поперечной сил, а параметры mx1, my1, mx1 - коэффициентами моментов крена, рыскания и тангажа.
Из анализа выражений для аэродинамических сил (1.3.2) -:- (1.3.4) следует вывод, что каждую из этих сил можно разделить на составляющую, обусловленную давлением, и составляющую, связанную с касательными напряжениями, возникающими при движении вязкой жидкости. Например, лобовое сопротивление X=XP+Xf: первая составляющая (XP) называется сопротивлением давления, вторая (Xf) - сопротивлением трения. Согласно этому полный коэффициент сопротивления равен сумме коэффициентов сопротивлений давления и трения: cx=cxp+cxf.
Аналогично можно представить в виде суммы двух составляющих аэродинамические коэффициенты подъемной и боковой сил, а также моментов. Таким же образом записываются силы, моменты и их коэффициенты в связанных осях. Например, коэффициент продольной силы cR=cRp+cRf (где cRp, cRf - коэффициенты продольных сил соответственно от давления и трения).
Составляющие аэродинамических сил и моментов, зависящие от трения, не всегда по порядку величин такие, как составляющие от давления. Исследования показывают, что влияние трения оказывается более существенным в случае обтекания длинных и тонких тел. При этом в практических случаях такое влияние целесообразно учитывать в основном при определении сопротивления (продольной силы).
При наличии у обтекаемой поверхности плоской площадки в хвостовой части (донный срез корпуса или затупленная задняя кромка крыла) сопротивление от давления обычно разделяют еще на две составляющие, а именно: сопротивление от давления на боковую поверхность (головное сопротивление) и сопротивление от давления на донный срез (донное сопротивление). В соответствии с этим суммарное сопротивление и соответствующий аэродинамический коэффициент равны:
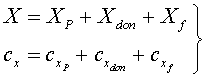
При определении продольной (осевой) силы и ее коэффициента можно написать:
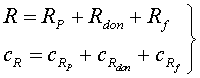
В соответствии с рис. 1.3.1
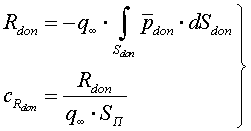
где
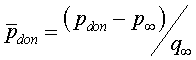(эта
величина отрицательная, так как за донным
срезом возникает разрежение, т. е. Pdon<pҐ.
Влияние донного давления на подъемную и
боковую силы, а также моменты, как правило,
оказывается пренебрежимо малым.